Sliding Window Technique

The sliding window technique is a fundamental algorithmic concept that I've found incredibly useful for solving a variety of problems efficiently. It involves maintaining a subset of elements from a given data structure (usually an array or list) and moving (or "sliding") this subset over the data structure to process it incrementally. This approach can significantly reduce the complexity of problems that require processing contiguous subarrays or substrings.

Key Concepts

1. Fixed-Size Sliding Window

In the fixed-size sliding window approach, the window has a constant size that does not change during the process. This is commonly used for problems where we need to find the maximum, minimum, or average of all subarrays of a fixed length.

Example: Finding the maximum sum of all subarrays of a given length in an array.

2. Variable-Size Sliding Window

In the variable-size sliding window approach, the window size can change dynamically based on the problem constraints. This technique is often used for problems that involve finding the smallest or largest window that satisfies a certain condition.

Example: Finding the smallest subarray with a sum greater than or equal to a given value.

Applications

• String Manipulation: Finding the longest substring without repeating characters, checking for anagrams, etc.
• Array Processing: Maximum or minimum values in subarrays, sum of subarrays, etc.
• Network Monitoring: Calculating moving averages or detecting anomalies in a stream of data packets.
• Image Processing: Sliding window for object detection, filtering, etc.

By utilizing the sliding window technique, I've been able to solve many problems that initially seemed complex in a more efficient and elegant way.

3. Longest Substring Without Repeating Characters

Given a string s, find the length of the longest substring without repeating characters.

Complete solution

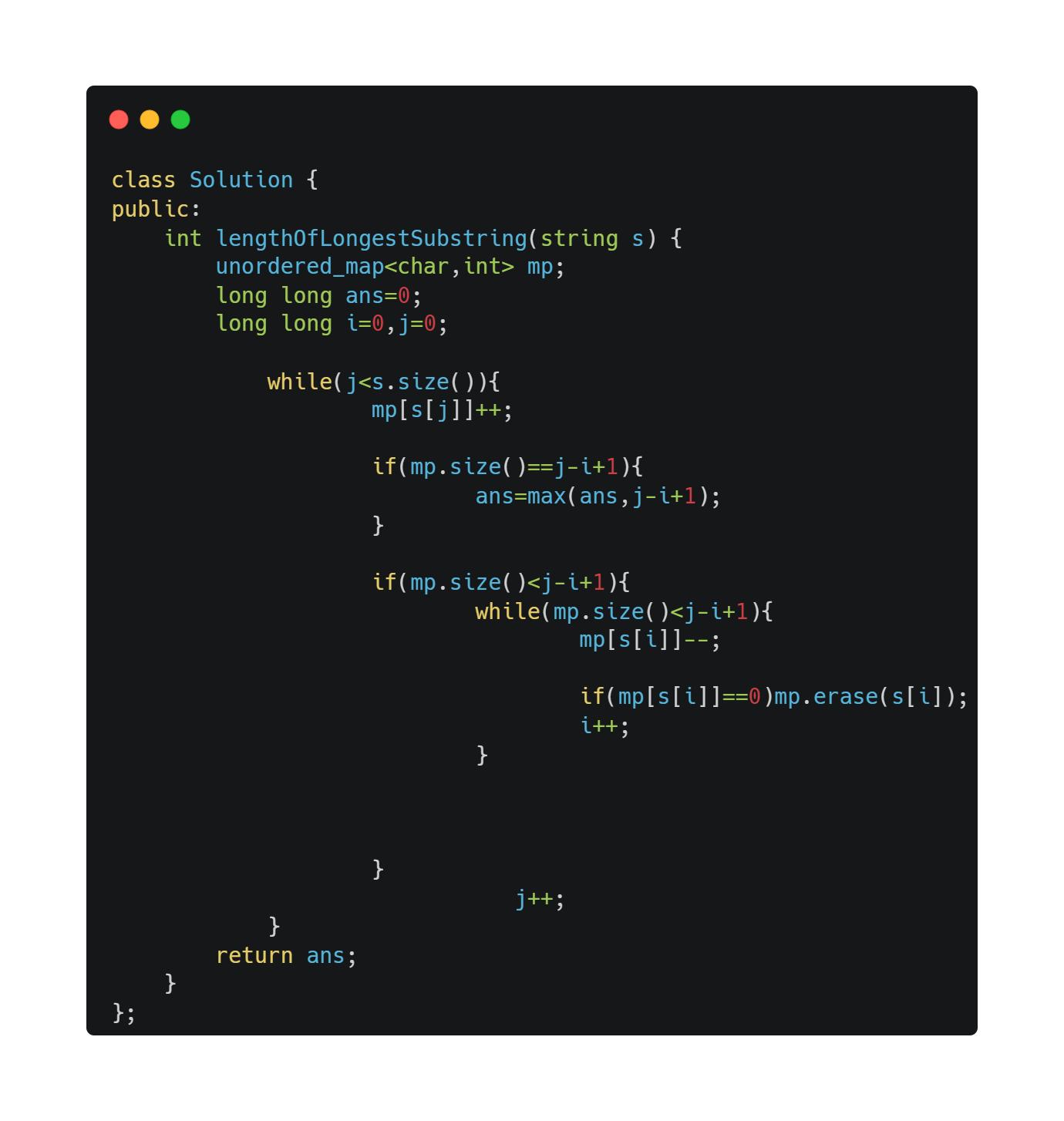
Line 2:unordered_map<char,int> mp;

I declare an unordered map mp to keep track of the frequency of characters in the current window. This helps me quickly check and update the count of each character.

Line 3:long long ans=0;

I initialize a variable ans to 0, which will store the length of the longest substring found without repeating characters.

Line 4:long long i=0,j=0;

I initialize two pointers i and j to 0. These pointers will represent the start and end of the current window, respectively.

Line 6:while(j<s.size())

I start a while loop that will continue until the j pointer reaches the end of the string s. This loop is used to expand the window by moving the j pointer.

Line 7:mp[s[j]]++;

I increment the frequency of the character at the jth position in the unordered map mp. This adds the character to the current window and updates its count.

Line 9:if(mp.size()==j-i+1)

I check if the size of the map mp is equal to the current window size (j-i+1). If this condition is true, it means all characters in the window are unique.

Line 10:ans=max(ans,j-i+1);

If the condition is true, I update the ans with the maximum value between the current ans and the current window size (j-i+1). This ensures that I keep track of the longest substring found so far.

Line 12:if(mp.size()<j-i+1)

If the size of the map mp is less than the current window size (j-i+1), it means there are duplicate characters in the current window.

Line 13:while(mp.size()<j-i+1)

I start a while loop to shrink the window from the left until all characters in the window are unique. This loop will continue until the size of the map mp is equal to the window size.

Line 14:mp[s[i]]--;

I decrement the frequency of the character at the ith position in the unordered map mp. This reduces the count of the character as I move the left pointer.

Line 15:if(mp[s[i]]==0)mp.erase(s[i]);

If the frequency of the character at the ith position becomes 0, I erase it from the unordered map mp to ensure only unique characters remain in the window.

Line 16:i++;

I increment the i pointer to shrink the window from the left.

Line 19:j++;

I increment the j pointer to expand the window to the right, continuing the process of finding the longest substring without repeating characters.

Line 21:return ans;

Finally, I return the value of ans, which is the length of the longest substring without repeating characters found in the given string s.

Example Run of the Code

Let's go through the code using the example string s = "abcabcbb" to find the length of the longest substring without repeating characters.

Initial Setup

• unordered_map<char,int> mp; - An empty map to store character frequencies.
• long long ans = 0; - To keep track of the length of the longest substring.
• long long i = 0, j = 0; - Two pointers to represent the start and end of the window.

Execution Steps

Initial State

• i = 0, j = 0
• mp = ⦃⦄
• ans = 0

1. Step 1

• j = 0, character = 'a'
• mp = ⦃'a': 1⦄
• Since mp.size() == j - i + 1 (1 == 1), update ans:
• ans = max(ans, j - i + 1) = max(0, 1) = 1
• Move j to 1.

2. Step 2

• j = 1, character = 'b'
• mp = ⦃'a': 1, 'b': 1⦄
• Since mp.size() == j - i + 1 (2 == 2), update ans:
• ans = max(ans, j - i + 1) = max(1, 2) = 2
• Move j to 2.

3. Step 3

• j = 2, character = 'c'
• mp = ⦃'a': 1, 'b': 1, 'c': 1⦄
• Since mp.size() == j - i + 1 (3 == 3), update ans:
• ans = max(ans, j - i + 1) = max(2, 3) = 3
• Move j to 3.

4. Step 4

• j = 3, character = 'a'
• mp = ⦃'a': 2, 'b': 1, 'c': 1⦄
• Since mp.size() < j - i + 1 (3 < 4), adjust the window:
• While mp.size() < j - i + 1:
• Decrement mp['a'] and remove 'a' if its count is 0:
• mp = ⦃'a': 1, 'b': 1, 'c': 1⦄, i = 1
• Move i to 1, continue adjusting:
• mp = ⦃'a': 0, 'b': 1, 'c': 1⦄, i = 2
• Remove 'a': mp = ⦃'b': 1, 'c': 1⦄, i = 2
• Move j to 4.

5. Step 5

• j = 4, character = 'b'
• mp = ⦃'b': 2, 'c': 1⦄
• Since mp.size() < j - i + 1 (2 < 3), adjust the window:
• While mp.size() < j - i + 1:
• Decrement mp['b']:
• mp = ⦃'b': 1, 'c': 1⦄, i = 3
• Move i to 3, continue adjusting:
• mp = ⦃'b': 1, 'c': 0⦄, i = 4
• Remove 'c': mp = ⦃'b': 1⦄, i = 4
• Move j to 5.

6. Step 6

• j = 5, character = 'c'
• mp = ⦃'b': 1, 'c': 1⦄
• Since mp.size() == j - i + 1 (2 == 2), update ans:
• ans = max(ans, j - i + 1) = max(3, 2) = 3
• Move j to 6.

7. Step 7

• j = 6, character = 'b'
• mp = ⦃'b': 2, 'c': 1⦄
• Since mp.size() < j - i + 1 (2 < 3), adjust the window:
• While mp.size() < j - i + 1:
• Decrement mp['b']:
• mp = ⦃'b': 1, 'c': 1⦄, i = 5
• Move i to 5, continue adjusting:
• mp = ⦃'b': 1, 'c': 0⦄, i = 6
• Remove 'c': mp = ⦃'b': 1⦄, i = 6
• Move j to 7.

8. Step 8

• j = 7, character = 'b'
• mp = ⦃'b': 2⦄
• Since mp.size() < j - i + 1 (1 < 2), adjust the window:
• While mp.size() < j - i + 1:
• Decrement mp['b']:
• mp = ⦃'b': 1⦄, i = 7
• Move i to 7, continue adjusting:
• mp = ⦃'b': 0⦄, i = 8
• Remove 'b': mp = ⦃⦄, i = 8
• Move j to 8.

Final Output

After processing all characters in the string, the final value of ans is 3. This represents the length of the longest substring without repeating characters, which is "abc".